Tyres and Artificial Neural Networks – Pt1
Tyres pose the biggest question in the world of simulation.
The problem is akin to the infamous elephant in the room: it’s impossible not to notice it, but everyone pretends that it’s not there.
Everyone, without exception, from F1 down, must instead try to decipher, interpret, and finally understand how to virtualize this round and black object that is the tyre.
The tyre, which is actually a hyper-complex system in which interconnected chemical and mechanical processes generate forces that are fundamental to the behavior of all vehicles.
In the last two years Megaride, a start up company conducted at Federico II University of Naples, has taken to understanding the tyre and its behavior better than anyone else; it’s numerous awards worldwide and customers at the highest levels testify the impressive levels of their research and their products.
Megaride and Skydrive have formed a great partnership: we can ask Megaride anytime that we have questions relating to tyres and wish to have affordable data on real tyre structure.
And in any case, to build up a virtual tyre that works in the same manner as a real one is certainly no easy task.
It is a real challenge to manage to “translate” the data we have from the real tyre into a mathematical model that is able to run in our simulation environment.
The tyre-system is so complex that, in the last year, Skydrive had deepened the knowledge of a brand new powerful computing tool: Artificial Intelligence
THE REAL TYRE
The real world tyre is described by the renowned Professor Hans B. Pacejka as “Magic Formula”, a mathematical model that has some coefficients for each force and momentum and is able to sum up all the data from a test on a dynamic rig. All these elements are summarized in a .TIR file
Thanks to Magic Formula’s coefficients we are able to derive equations with which we can calculate how much force is generated as a function of a given load as the characteristic angles vary.
Easier to say: to understand how a real tire behaves, the producer of the tire has to give us one (or more) .TIR file(s). With these files we can derive and calculate traction, slip and every aspect of tyre specific behaviour.
But here we encounter the first problem…
Whilst a racing car manufacturer will give you all the information, of every component, to understand and predict the behaviour of any part of the car, the tyre manufacturer never gives anything to anyone.
For confidentiality issues, no tyre producer ever discloses the construction and performance characteristics of their product.
In an industry where there are very few manufacturers (no more than 12 companies around the globe) that have the technology and products that they sell to everyone around the world, there is no interest or benefit in disclosing their intellectual property. For this reason, since the time when the veterinarian John Dunlop invented the first tyre back in 1888, the various companies such as Bridgestone, Goodyear, Michelin, etc. provide any kind of tyre to any kind of vehicle, from a Fiat Panda to a Boeing 777, without divulging a thing!
But here, fortunately, we can work with Megaride and utilise its incredible abilities.
As nobody will give you the tyre characteristics, you have to find a way to infere them form a real rolling tyre. Only Megaride has found a way to do it, through analysis and dynamic tests, in a brand new way.
They are the only ones that can give us the description of the real tyre.
Problem 1: solved.
Let’s face the next one!
VIRTUAL TYRE
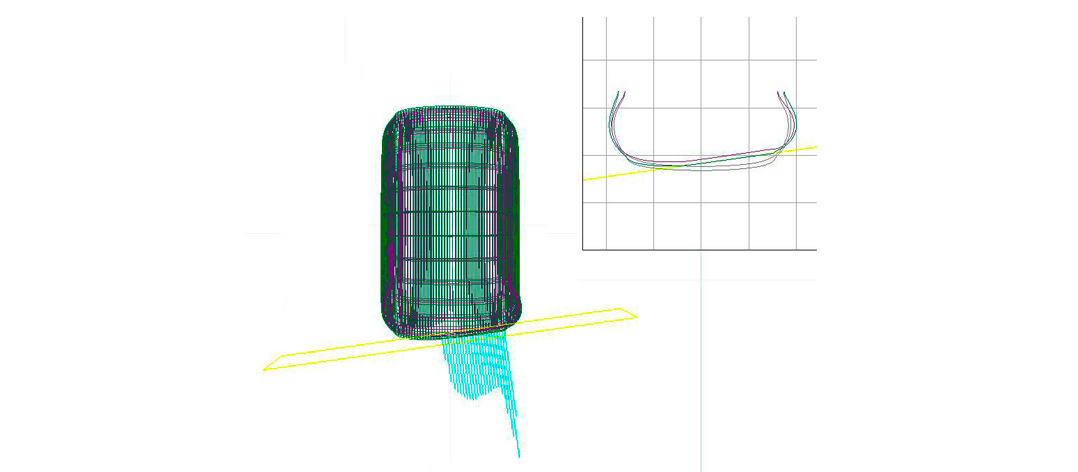
Let’s assume that we have a good .tir file that describes our real tyre. We just have to recreate the same tyre in our simulation environment.
Easy to say, almost impossible to do. Almost…
First of all, the virtual tyre model can not run with the .tir data, because the simulation environment in which it has to run has very specific systemic properties.
So, we have to build up a tyre that follows the logical path of the simulation environment and try to describe the tyre features to make it work exactly as the real one does, with the same levels of performance.
We have a physical object that, when stimulated in a certain way, generates certain reactions that we record in a .tir. file.
We have to create a virtual object, described mathematically according to a completely different system, which, when stimulated in the same way, generates the same reactions as the real one.
There is software, such as Matlab and others, that provide us with a computing environment with thousands of libraries of information especially developed for the most disparate sectors: structural, hydrodynamic, statistical calculations… in short, thanks to the matrices and its countless functions we can develop ad-hoc algorithms for any need.
With these programs we can “build” a virtual object that has specific characteristics, such as our tyre. This virtual tyre gives us outputs for each input, according to the established rules that we give.
It is as if, ideally, we are building a tyre and putting it on a test bench (or dynamic bench) to measure its performance.
Theoretically, we can “build” our object by describing its physical characteristics, solicit it by sending inputs (as we do on track with the real one) and see what type of output it will provide, and what performances also.
We can finally compare these performances with the ones generate by the .tir file.
At this point we have to reverse engineer the tyre, changing the characteristics of the virtual one until the outputs it generates are exactly the same as the real one.
Any time that a variable is changed, it is necessary to make a test (in Mathlab) and then compare the outputs with the ones generated by the real tyre.
At this point we find an enormous calculation problem, which is really the heart of the question.
Even if we consider only 16 variable (the 16 most important variables, like stiffness, damping, inertia…) we have to make an incredibly high number of tests, more or less 1016.
Anytime we add a variable we have to add one element to our calculation matrix, that makes the number of the tests exponentially grow.
The total number of variables is 36: we can perform exponentiation till the 36th power, that means we would have to make 1036 tests.
Even with a lot of good will, it would take tens of years to process this type of calculation with normal tools. Or we have to employ computers with enormous computing power, as big as your living room and as expensive as a Space X.
After a long and in-depth analysis of this calculation problem, we at Skydrive have considered all the calculation possibilities as of now, and we have chosen a “black-box modeling technique” approach, that is a computational modeling technique developed in the Neural Network context.
It is here that the Artificial Intelligence finally arrives.
WHAT IS AN ARTIFICIAL NEURAL NETWORK
An Artificial Neural Network (ANN) is, technically, a type of Machine Learning, that is part of the AI world. 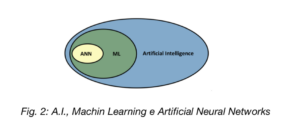
As a biological neural network does, an ANN can literally learn through the acquisition of a large amount of data, it can find patterns and organize them in a hierarchy by their futures. That’s the way a ANN can solve extremely complex duties.
The technique chosen by Skydrive, the black-box technique, is a way to create a model of a system (as the tyre-system) starting from the way that the system reacts to an input.
The ANN rebuilt the relation between input and output starting from the data, without using any equation.
That is the meaning of “black-box”: you don’t need to know what’s inside the box, but just what the inputs are and what the outputs are.
The ANN will rebuild this relationship.
In this way the ANN can manage very complex and non-linear systems, not know how they are structured, and it can organize a vast amount of data.
That’s exactly what we were looking for from our “Tyre Problem”, assuming that the tyre is a high complex, non-linear system, with a high numbers of variables.
CONTINUES
